Se define como movimiento circular aquél cuya trayectoria es una circunferencia.
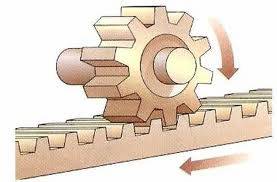 |
El movimiento circular del piñón se transforma en
movimiento lineal en la cremallera. |
El movimiento circular, llamado también curvilíneo, es otro tipo de movimiento sencillo.
Estamos rodeados por objetos que describen movimientos circulares: un disco compacto durante su reproducción en el equipo de música, las manecillas de un reloj o las ruedas de una motocicleta son ejemplos de movimientos circulares; es decir, de cuerpos que se mueven describiendo una circunferencia.
A veces el movimiento circular no es completo: cuando un coche o cualquier otro vehículo toma una curva realiza un movimiento circular, aunque nunca gira los 360º de la circunferencia.
La experiencia nos dice que todo aquello da vueltas tiene movimiento circular. Si lo que gira da siempre el mismo número de vueltas por segundo, decimos que posee movimiento circular uniforme (MCU).
Ejemplos de cosas que se mueven con movimiento circular uniforme hay muchos:
La tierra es uno de ellos. Siempre da una vuelta sobre su eje cada 24 horas. También gira alrededor del sol y da una vuelta cada 365 días. Un ventilador, un lava ropas o los viejos tocadiscos, la rueda de un auto que viaja con velocidad constante, son otros tantos ejemplos.
VELOCIDAD ANGULAR (ω)
Cuando un objeto se mueve en una circunferencia, llevará una velocidad, ya que recorre un espacio, pero también recorre un ángulo.
Para tener una idea de la rapidez con que algo se está moviendo con movimiento circular, se ha definido la velocidad angular (ω) como el número de vueltas que da el cuerpo por unidad de tiempo.
Si un cuerpo tiene gran velocidad angular quiere decir que da muchas vueltas por segundo.
De manera sencilla: en el movimiento circular la velocidad angular está dada por la cantidad de vueltas que un cuerpo da por segundo.
Otra manera de decir lo mismo sería: en el movimiento circular la velocidad angular está dada por el ángulo recorrido (θ) dividido por unidad de tiempo. El resultado está en grados por segundo o en rad por segundo.
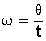
ω = velocidad angular en rad/seg.
θ = desplazamiento angular en rad.
t = tiempo en segundos en que se efectuó el desplazamiento angular.
La velocidad angular también se puede determinar si sabemos el tiempo que tarda en dar una vuelta completa o periodo (T):
Como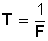 entonces
entonces 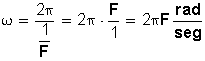
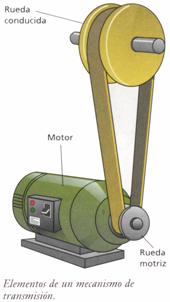 |
| Trasmisión de un movimiento circular. |
Aquí debemos apuntar que una misma velocidad angular se puede expresar de varias maneras diferentes.
Por ejemplo, para las lavadoras automáticas o para los motores de los autos se usan lasrevoluciones por minuto (rpm). También a veces se usan las rps (revoluciones por segundo).
También se usan los grados por segundo y los radianes por segundo.
Es decir, hay muchas unidades diferentes de velocidad angular. Todas se usan y hay que saber pasar de una a otra, lo que se hace aplicando una regla de 3 simple.
Por ejemplo, pasar una velocidad de 60 rpm a varias unidades diferentes:
La más importante de todas las unidades de velocidad angular es radianes por segundo. Esta unidad es la que se usa en los problemas.
Nota importante:
Según lo anterior es correcto, entonces, decir que la velocidad angular es
 , pero resulta que el radián es sólo un número comparativo, por lo mismo que la palabra radián suele no ponerse y en la práctica la verdadera unidad es
, pero resulta que el radián es sólo un número comparativo, por lo mismo que la palabra radián suele no ponerse y en la práctica la verdadera unidad es , que también puede ponerse como
, que también puede ponerse como 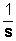 , e incluso como
, e incluso como 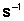 .
.
En efecto, muchas veces la velocidad angular se expresa en segundos elevado a menos uno (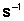 ) y para quienes no lo saben resulta incomprensible.
) y para quienes no lo saben resulta incomprensible.
ACELERACIÓN ANGULAR
Tal como el movimiento lineal o rectilíneo, el movimiento circular puede ser uniforme o acelerado. La rapidez de rotación puede aumentar o disminuir bajo la influencia de un momento de torsión resultante.
La aceleración angular (α) se define como la variación de la velocidad angular con respecto al tiempo y está dada por:
donde:
α = aceleración angular final en rad/ s2
ωf = velocidad angular final en rad/s
ωi = velocidad angular inicial en rad/s
t = tiempo transcurrido en seg
Una forma más útil de la ecuación anterior es:
ωf = ωi + α t
FUERZA CENTRÍPETA
Los objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con rapidez constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por
Donde:
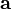 es la aceleración centrípeta.
es la aceleración centrípeta. es el módulo de la velocidad.
es el módulo de la velocidad. es el radio de la trayectoria circular (en general, el radio de curvatura).
es el radio de la trayectoria circular (en general, el radio de curvatura).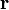 el vector de posición.
el vector de posición.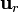 el versor radial.
el versor radial. la velocidad angular.
la velocidad angular.

CAMPO GRAVITATORIO
Se considera que una masa M modifica de algún modo el espacio. A este espacio perturbado por la masa se
llama campo gravitatorio, y se considera que actúa sobre cualquier otra masa m ejerciendo la fuerza de atracción
gravitatoria sobre ella, según establece la ley de la gravitación universal:
La intensidad de campo gravitatorio creado por una masa M en un punto representa la fuerza que
actuaría sobre la unidad de masa colocada en dicho punto. Matemáticamente:
De este modo, cada punto del espacio queda caracterizado por un valor de g , independiente de la masa m que se coloque en el punto, dependiente sólo de factores propios del campo (la masa M que lo crea y la distancia r al punto considerado). La intensidad de campo gravitatorio representa la aceleración que adquiriría un cuerpo situado en un punto del campo (la conocida gravedad). Al colocar en los alrededores de M una masa m, la fuerza que aparece sobre ella es:
Dado el carácter vectorial del campo, se cumple el principio de superposición: el campo gravitatorio creado en un punto por varias masas es la composición vectorial de los campos individuales generados en ese punto por cada una de ellas, es decir:
SATÉLITES EN ÓRBITA GRAVITATORIA
En un sistema gravitatorio cerrado o aislado, es decir, en un sistema en el que las únicas fuerzas presentes son las debidas a la interacción gravitatoria entre sus constituyentes, se satisface que la suma de la energía cinética y la energía potencial gravitatoria permanece constante (ley de conservación de la energía mecánica en ausencia de fuerzas disipativas). Así, para una masa que se traslada desde una posición A hasta una posición B dentro de un campo gravitatorio se debe cumplir:

La energía cinética siempre es positiva; su menor valor posible, el cero, corresponde a un cuerpo en reposo. La energía potencial gravitatoria siempre es negativa; su máximo valor posible, el cero, corresponde a una
separación infinita entre los constituyentes del sistema. Teniendo en cuenta esto, si la energía mecánica es negativa significa que el cuerpo de menos masa órbita en torno al objeto de más masa, ya que sólo podrá separarse de él hasta una cierta distancia; se trata de un sistema gravitatorio ligado. Por el contrario, cuando la energía mecánica es nula o positiva, los cuerpos pueden llegar a estar separados una distancia infinita; se trata de un sistema gravitatorio libre.
Un sistema gravitatorio modifica su energía mecánica cuando sobre alguno de sus constituyentes actúa una
interacción no gravitatoria. El trabajo exterior que realizan las fuerzas no gravitatorias se identifica con la energía
necesaria para realizar una determinada transformación (levantar un objeto, poner un satélite en órbita,…): (ley de conservación de la energía mecánica en presencia de fuerzas no conservativas).
(ley de conservación de la energía mecánica en presencia de fuerzas no conservativas).
LANZAMIENTO DE SATÉLITES EN ÓRBITA GRAVITATORIA
Una de las aplicaciones más importantes del campo gravitatorio se inició en 1957 cuando los soviéticos pusieron en órbita el satélite artificial Sputnik (en ruso significa “compañero de viaje”). El proceso siguió en 1961 cuando Yuri Gagarin permaneció durante 1h 40 min en órbita alrededor de la Tierra. Después tuvo lugar el primer paseo espacial de Alexéi Leonov en 1965, la llegada de Armstrong y Aldrin a la Luna el 20 de julio de 1969, el primer vuelo del trasbordador espacial en 1981, la puesta en órbita de la estación espacial soviética Mir en 1986, o del primer módulo de la futura estación espacial internacional (ISS) en 1998,..., acontecimientos que han permitido denominar este tiempo como era espacial. Hoy son miles los satélites en órbita alrededor de la Tierra (sin olvidar los restos de cohetes, fragmentos de satélites, etc.) con distintas y múltiples funciones que cumplir: desarrollar las telecomunicaciones, obtener información meteorológica, militar, adquirir nuevos conocimientos científicos, tanto sobre la Tierra (temperatura superficiales, capa de ozono, vegetación, desertización, etc.) como sobre el espacio exterior (existencia de otras galaxias, agujeros negros, estrellas de neutrones, etc.).
El proceso de puesta en órbita de un satélite artificial consta de varias etapas. En primer lugar se lanza desde una base cercana al ecuador terrestre y hacia el este para aprovechar el movimiento de rotación de la Tierra. A continuación, y por ahorro energético, el satélite se sitúa en una órbita muy excéntrica, con su perigeo en torno a los 300 km de la superficie de la Tierra.
Cuando el satélite pasa por su apogeo, punto más alejado de la órbita, se aumenta su velocidad hasta situarlo en la órbita definitiva. Otra forma de colocar un satélite en órbita es mediante un trasbordador espacial tripulado, que realizará otras misiones de investigación. Cuando se alcanza la órbita prevista, se le comunica al satélite la velocidad tangencial adecuada para que continúe su trayectoria.
Nos podemos encontrar satélites geosíncronos o geoestacionarios y satélites heliosíncronos (figura 9):
- Los satélites geoestacionarios describen órbitas circulares en el plano ecuatorial con un período de 24 horas, por lo que se encuentran siempre sobre el mismo punto de la superficie terrestre. Estas condiciones implican una elevada altitud para la órbita (35.900 km sobre la superficie terrestre), lo que hace que no puedan obtener imágenes de alta resolución de la Tierra;
por eso se usan fundamentalmente para aplicaciones meteorológicas, de comunicaciones y de investigación del espacio exterior (satélites METEOSAT, GOES, GMS, …).
- Los satélites heliosíncronos describen órbitas cuasipolares aprovechando la no esfericidad del campo gravitatorio terrestre.
Las órbitas heliosíncronas mantienen constante el ángulo que forma el plano de la órbita y la dirección Sol-Tierra, lo que facilita el diseño del satélite (orientación de las placas solares y de los aislantes térmicos) y, lo que es más importante, el satélite pasa siempre sobre la misma zona a la misma hora local, lo que facilita enormemente la comparación de medidas tomadas en distintas pasadas. Los satélites de exploración terrestre recorren órbitas heliosíncronas a alturas entre 300 km y 1.200 km (frecuentemente en torno a los 850 km) (satélites LANDSAT, SPOT, NOAA, ERS, ENVISAT, IKONOS, QUICKBIRD, GALILEO, …). Teniendo en cuenta los conocimientos adquiridos, abordamos los problemas físicos que se plantean al lanzar y mantener en órbita los cohetes y satélites artificiales.
EJERCICIOS ACERCA DEL CAMPO GRAVITATORIO:
MÁS INFORMACIÓN ACERCA DEL TEMA:
 .
. ).
). ).
). .
.



 es el momento aplicado al cuerpo.
es el momento aplicado al cuerpo. es el momento de inercia del cuerpo con respecto al eje de rotación y
es el momento de inercia del cuerpo con respecto al eje de rotación y es la aceleración angular.
es la aceleración angular.

 tiene como equivalente para la rotación:
tiene como equivalente para la rotación: tiene como equivalente para la rotación:
tiene como equivalente para la rotación: , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es
, mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es  . Donde I es el momento de inercia con respecto al eje de rotación.
. Donde I es el momento de inercia con respecto al eje de rotación. , mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es
, mientras que la energía de cinética de un cuerpo en rotación con velocidad angular ω es  . Donde I es el momento de inercia con respecto al eje de rotación.
. Donde I es el momento de inercia con respecto al eje de rotación. :
: :
: .
. .
.



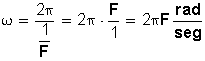


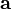 es la aceleración centrípeta.
es la aceleración centrípeta. es el módulo de la velocidad.
es el módulo de la velocidad. es el radio de la trayectoria circular (en general, el radio de curvatura).
es el radio de la trayectoria circular (en general, el radio de curvatura).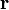 el vector de posición.
el vector de posición.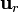 el versor radial.
el versor radial. la velocidad angular.
la velocidad angular. en
en





