Gravedad y Caída libre de los cuerpos (Tiro Parabólico)

„Para entender el concepto de caída libre de los cuerpos, veremos el siguiente ejemplo: Si dejamos caer una pelota de hule macizo y una hoja de papel, al mismo tiempo y de la misma altura, observaremos que la pelota llega primero al suelo. Pero, si arrugamos la hoja de papel y realizamos de nuevo el experimento observaremos que los tiempos de caída son casi iguales. 

El movimiento vertical de cualquier objeto en movimiento libre, para el que se pueda pasar por esto la resistencia del aire, se resume entonces mediante las ecuaciones:

„a). v = -gt + v0 

b). Vm = (vo + v)/2 

c). y = -0.5 gt² + vo t + y0 

d). v²= -2gt (y - y0) 

Trayectoria. Es la sucesión de puntos por los que pasó el móvil en su recorrido y su valor en el Sistema Internacional es esa distancia, medida sobre la trayectoria, en metro. Es el recorrido total. 

Posición. Supuestos unos ejes de coordenadas en el punto de lanzamiento, se llama posición a la ordenada (coordenada en el eje y) que ocupa en cada instante el móvil. 

Desplazamiento. Restando de la ordenada de la posición la ordenada del origen tenemos el desplazamiento. Se representa por un vector con todas las características del mismo: modulo, dirección, sentido, punto de aplicación.

En cinemática, la caída libre es un movimiento de un cuerpo dónde solamente influye la gravedad. En este movimiento se desprecia el rozamiento del cuerpo con el aire, es decir, se estudia en el vacío. El movimiento de la caída libre es un movimiento uniformemente acelerado. La aceleración instantánea es independiente de la masa del cuerpo, es decir, si dejamos caer un coche y una pulga, ambos cuerpo tendrán la misma aceleración, que coincide con la aceleración de la gravedad (g). Esto lo podemos demostrar del siguiente modo:

Sabemos por la segunda ley de Newton que la fuerza es igual al producto entre la masa del cuerpo y la aceleración.

             F = ma

La única fuerza que influye en la caída libre (recordamos que se desprecia el rozamiento con el aire) es el peso, que es igual al producto entre la masa del cuerpo y la constante gravitatoria g.

      F = P = mg

Despejamos de la primera ecuación la aceleración.

        F

 a = m

Sustituimos la fuerza.

        mg

 a  =    m

Por lo tanto nos queda que la aceleración del cuerpo siempre coincide con la constante gravitatoria

  a = g

Otra forma de demostrar que la aceleración de los cuerpos en caída libre en el vacío tiene que ser la misma sin importar el peso de los objetos, es mediante un simple desarrollo lógico:  Supongamos dos cuerpos, el primero del doble de peso que el segundo. Ahora, interpretemos al primer objeto como dos de los segundos objetos unidos de alguna forma, entonces la aceleración del objeto más pesado debería ser la misma que la de cada uno de los dos objetos más livianos, puesto que si así no fuera entonces un cuerpo debería caer a diferentes velocidades dependiendo de si lo vemos como un solo objeto o como sus partes unidas.

Tiro parabólico

Galileo Galilei estudio y dedujo ecuaciones  del tiro de proyectiles. 

El tiro parabólico es un movimiento que resulta de la unión de dos movimientos: El movimiento rectilíneo uniforme (componentes horizontal)  y, el movimiento vertical  (componente vertical) que se efectúa por la gravedad y el resultado de este movimiento es una parábola.   

El tiro parabólico, es  la  resultante de la suma vectorial de un movimiento horizontal uniforme y  de  un  movimiento vertical rectilíneo uniformemente variado. El tiro parabólico es de dos clases:  a) tiro horizontal y, b) tiro oblicuo 

a)  Tiro Horizontal    

 Se caracteriza por la trayectoria curva  que sigue un cuerpo al ser lanzado horizontalmente al vació. 

El  resultado  de  dos movimientos independientes: un movimiento horizontal con velocidad constante y un movimiento vertical que se inicia con una velocidad 0 y va aumentando, en  proporción de otro cuerpo que se dejara caer del mismo punto en el mismo instante  

DH= vHt

Donde:

dH  =  distancia horizontal

vH  =  velocidad horizontal

  t  =  tiempo de caída 

b) Tiro oblicuo

Se caracteriza por la trayectoria que sigue un cuerpo, cuando es lanzado a una velocidad inicial que forma un ángulo 𝜃 con el eje horizontal. 

Las componentes vertical y horizontal de la velocidad, tienen un valor al inicio de su movimiento que se calcula con las siguientes fórmulas 

Trabajo, potencia y energría

Trabajo

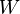En mecánica clásica, el trabajo que realiza una fuerza sobre un cuerpo equivale a la energía necesaria para desplazar este cuerpo. El trabajo es una magnitud física escalar que se representa con la letra  (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.

Ya que por definición el trabajo es un tránsito de energía, nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.

Matemáticamente se expresa como:

Donde  es el módulo de la fuerza,  es el desplazamiento y  es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).

Cuando el vector fuerza es perpendicular al vector desplazamiento del cuerpo sobre el que se aplica, dicha fuerza no realiza trabajo alguno. Asimismo, si no hay desplazamiento, el trabajo también será nulo.

Potencia

En física, potencia (símbolo P)^{nota 1} es la cantidad de trabajo efectuado por unidad de tiempo.

Si W es la cantidad de trabajo realizado durante un intervalo de tiempo de duración Δt, la potencia media durante ese intervalo está dada por la relación:

La potencia instantánea es el valor límite de la potencia media cuando el intervalo de tiempo Δt se aproxima a cero:

Donde:

• P es la potencia,
• W es el trabajo,
• t es el tiempo.
• r es el vector de posición.
• F es la fuerza.
• v es la velocidad.

Energía

El término energía (del griego ἐνέργεια/energeia, actividad, operación; ἐνεργóς/energos = fuerza de acción o fuerza trabajando) tiene diversas acepciones y definiciones, relacionadas con la idea de una capacidad para obrar, transformar o poner en movimiento.

En física, «energía» se define como la capacidad para realizar un trabajo.

Capacidad de un sistema físico para realizar trabajo. La materia posee energía como resultado de su movimiento o de su posición en relación con las fuerzas que actúan sobre ella. La radiación electromagnética posee energía que depende de su frecuencia y, por tanto, de su longitud de onda. Esta energía se comunica a la materia cuando absorbe radiación y se recibe de la materia cuando emite radiación. La energía asociada al movimiento se conoce como energía cinética, mientras que la relacionada con la posición es la energía potencial. Por ejemplo, un péndulo que oscila tiene una energía potencial máxima en los extremos de su recorrido; en todas las posiciones intermedias tiene energía cinética y potencial en proporciones diversas. La energía se manifiesta en varias formas, entre ellas la energía mecánica, térmica, química, eléctrica, radiante o atómica. Todas las formas de energía pueden convertirse en otras formas mediante los procesos adecuados. En el proceso de transformación puede perderse o ganarse una forma de energía, pero la suma total permanece constante.

Leyes de Newton

PRIMERA LEY DE NEWTON O LEY DE INERCIA:

Es la capacidad que poseen los cuerpos para resistir el cambio en su estado, ya sea esté en movimiento o en reposo. Si está en reposo, tratan de continuar así y si están en movimiento tratan de permanecer en ese estado. 

Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante. 

En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial. 

segunda ley de newton:

La segunda ley del movimiento de Newton dice que:

El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.

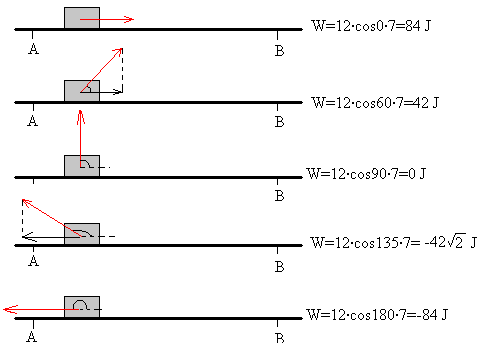
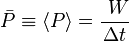
Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y el efecto, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.

En términos matemáticos esta ley se expresa mediante la relación:

Donde:

 es el momento lineal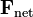

 la fuerza total o fuerza resultante.

Suponiendo que la masa es constante y que la velocidad es muy inferior a la velocidad de la luz⁸ la ecuación anterior se puede reescribir de la siguiente manera:

Sabemos que  es el momento lineal, que se puede escribir m.V donde m es la masa del cuerpo y V su velocidad.

Consideramos a la masa constante y podemos escribir  aplicando estas modificaciones a la ecuación anterior: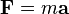

La fuerza es el producto de la masa por la aceleración, que es la ecuación fundamental de la dinámica, donde la constante de proporcionalidad, distinta para cada cuerpo, es su masa de inercia. Veamos lo siguiente, si despejamos m de la ecuación anterior obtenemos que m es la relación que existe entre  y . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.

Por tanto, si la fuerza resultante que actúa sobre una partícula no es cero, esta partícula tendrá una aceleración proporcional a la magnitud de la resultante y en dirección de ésta. La expresión anterior así establecida es válida tanto para la mecánica clásica como para la mecánica relativista, a pesar de que la definición de momento lineal es diferente en las dos teorías: mientras que la dinámica clásica afirma que la masa de un cuerpo es siempre la misma, con independencia de la velocidad con la que se mueve, la mecánica relativista establece que la masa de un cuerpo aumenta al crecer la velocidad con la que se mueve dicho cuerpo.

De la ecuación fundamental se deriva también la definición de la unidad de fuerza o newton (N). Si la masa y la aceleración valen 1, la fuerza también valdrá 1; así, pues, el newton es la fuerza que aplicada a una masa de un kilogramo le produce una aceleración de 1 m/s². Se entiende que la aceleración y la fuerza han de tener la misma dirección y sentido.

La importancia de esa ecuación estriba sobre todo en que resuelve el problema de la dinámica de determinar la clase de fuerza que se necesita para producir los diferentes tipos de movimiento:rectilíneo uniforme (m.r.u), circular uniforme (m.c.u) y uniformemente acelerado (m.r.u.a).

Si sobre el cuerpo actúan muchas fuerzas, habría que determinar primero el vector suma de todas esas fuerzas. Por último, si se tratase de un objeto que cayese hacia la tierra con una resistencia del aire igual a cero, la fuerza sería su peso, que provocaría una aceleración descendente igual a la de la gravedad.

TERCERA LEY DE newton O LEY DE ACCIÓN Y REACCIÓN: 

Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros. 

La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario. 

Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba. 

Cuando estamos en una piscina y empujamos a alguien, nosotros también nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros. 

Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actúan sobre cuerpos distintos. 

 

Condiciones de equilibrio

Una condición de equilibrio implica que una fuerza aislada aplicada sobre un cuerpo no puede producir por sí sola equilibrio y que, en un cuerpo en equilibrio, cada fuerza es igual y opuesta a la resultante de todas las demás. Así, dos fuerzas iguales y opuestas, actuando sobre la misma línea de acción, sí producen equilibrio. 

El equilibrio puede ser de tres clases: estable, inestable e indiferente. Si un cuerpo está suspendido, el equilibrio será estable si el centro de gravedad está por debajo del punto de suspensión; inestable si está por encima, e indiferente si coinciden ambos puntos. Si un cuerpo está apoyado, el equilibrio será estable cuando la vertical que pasa por el centro de gravedad caiga dentro de su base de sustentación; inestable cuando pase por el límite de dicha base, e indiferente cuando la base de sustentación sea tal que la vertical del centro de gravedad pase siempre por ella. 

Análisis del equilibrio

La estática proporciona, mediante el empleo de la mecánica del sólido rígido, solución a los problemas denominados isostáticos. En estos problemas, es suficiente plantear las condiciones básicas de equilibrio, que son: 

1. El resultado de la suma de fuerzas es nulo. 

2. El resultado de la suma de momentos respecto a un punto es nulo. 

• Estas dos condiciones, mediante el álgebra vectorial, se convierten en un sistema de ecuaciones; la resolución de este sistema de ecuaciones es la solución de la condición de equilibrio. 
• Existen métodos de resolución de este tipo de problemas estáticos mediante gráficos, heredados de los tiempos en que la complejidad de la resolución de sistemas de ecuaciones se evitaba mediante la geometría, si bien actualmente se tiende al cálculo por ordenador. 

Para la resolución de problemas hiperestáticos (aquellos en los que el equilibrio se puede alcanzar con distintas combinaciones de esfuerzos) es necesario considerar ecuaciones de compatibilidad. Dichas ecuaciones adicionales de compatibilidad se obtienen mediante la introducción de deformaciones y tensiones internas asociadas a las deformaciones mediante los métodos de la mecánica de sólidos deformables, que es una ampliación de la mecánica del sólido rígido que, además, da cuenta de la deformidad de los sólidos y sus efectos internos. 

Existen varios métodos clásicos basados en la mecánica de sólidos deformables, como los teoremas de Castigliano o las fórmulas de Navier-Bresse. 

Primera Condición de Equilibrio:

"Un cuerpo se encuentra en equilibrio de traslación, si la fuerza resultante de todas las fuerzas externas que actúan sobre él es nulo."

Matemáticamente:

Para el caso de fuerzas coplanares que se encuentran en el plano cartesiano xy se reduce la fuerza resultante en cada uno de los ejes x e y es cero: 

 

Geométricamente esto implica que estas fuerzas, al ser graficadas una a continuación de la otra, de modo tal que el extremo de cada una coincida con el origen de otra, formen un polígono cerrado. 

 

Para el caso particular que sobre el cuerpo actúan solo tres fuerzas, estas deben formar un triángulo de fuerzas. 

 

PROBLEMA 

Si la esfera mostrada en la figura es de 20N, y el módulo de la fuerza F aplicada es de 80 N, determinar los módulos de las reacciones del apoyo en A y B. 

 

Hagamos DCL de la esfera teniendo presente que las reacciones del apoyo en A y B son perpendiculares a las superficies en contacto y se grafican "entrando" al cuerpo que se analiza. 

 

Teniendo presente que los ángulos de la dos perpendiculares son iguales, deducimos que la reacción del apoyo en A (RA) forma con la vertical un ángulo que es igual al ángulo diedro 2θ. 

Por otro lado, tenido presente que los ángulos alternos internos entre rectas paralelas son iguales, deducimos que la fuerza F forma con la horizontal un ángulo θ. 

A continuación construyamos el triángulo de fuerzas tenido presente que la resultante de la reacción del apoyo en B y el peso apunta hacia arriba. 

 

Se comprueba que el triángulo de fuerzas es un triángulo equilátero y por tanto: 

 

PROBLEMA: Una pelota de 300N cuelga atada a otras dos cuerdas, como se observa en la figura. Encuentre las tensiones en las cuerdas A, B Y C. 

  

SOLUCIÓN: 

El primer paso es construir un diagrama de cuerpo libre: 

 

  

Al sumar las fuerzas a lo largo del eje X obtenemos : 

S Fx = -A cos 60° + B cos 40° = 0 

  

Al simplificarse por sustitución de funciones trigonométricas conocidas tenemos: 

-0.5A + 0.7660B = 0 (1) 

  

Obtenemos una segunda ecuación sumando las fuerzas a lo largo del eje Y, por lo tanto tenemos: 

(Cos 30° + cos 50° ) 

0.8660A + 0 .6427B = 300N (2)  

En las ecuaciones 1 y 2 se resuelven como simultanea A y B mediante el proceso de sustitución. Si despejamos A tenemos: 

A = 0.7660 / 0.5 

 A = 1.532B  

Ahora vamos a sustituir esta igualdad en la ecuación 2 

0.8660(1.532B) + 0.6427B = 300N 

  

Para B tenemos: 

1.3267B + 0.6427B = 300N 

  

1.9694B = 300N 

B= 300N / 1.9694 

  

B= 152.33N 

  

Para calcular la tensión en A sustituimos B = 152.33 N 

A = 1.532(152.33N) = 233.3N 

      La tensión en la cuerda C es 300N , puesto que debe ser igual al peso.  

Segunda Condición de Equilibrio:

"La suma algebraica de los momentos o torques de todas las fuerzas respecto a un punto cualquiera es igual a cero."

Momento o torque de una fuerza 

Cuando se aplica una fuerza en algún punto de un cuerpo rígido, dicho cuerpo tiende a realizar un movimiento de rotación en torno a algún eje. 

La puerta gira cuando se aplica una fuerza sobre ella; es una fuerza de torque o momento.

Ahora bien, la propiedad de la fuerza aplicada para hacer girar al cuerpo se mide con una magnitud física que llamamos torque o momento de la fuerza. 

Entonces, se llama torque o momento de una fuerza a la capacidad de dicha fuerza para producir un giro o rotación alrededor de un punto.  

En el caso específico de una fuerza que produce un giro o una rotación, muchos prefieren usar el nombre torque y no momento, porque este último lo emplean para referirse al momento lineal de una fuerza. 

Para explicar gráficamente el concepto de torque, cuando se gira algo, tal como una puerta, se está aplicando una fuerza rotacional. Esa fuerza rotacional es la que se denomina torque o momento. 

Cuando empujas una puerta, ésta gira alrededor de las bisagras. Pero en el giro de la puerta vemos que intervienen tanto la intensidad de la fuerza como su distancia de aplicación respecto a la línea de las bisagras.  

Entonces,  considerando estos dos elementos, intensidad de la fuerza y distancia de aplicación desde su eje, el momento de una fuerza  es, matemáticamente,  igual al producto de la intensidad de la fuerza (módulo) por la distancia desde el punto de aplicación de la fuerza hasta el eje de giro. 

Expresada como ecuación, la fórmula es 

 M = F • d 

Cuando se ejerce una fuerza F en el punto B de la barra, la barra gira alrededor del punto A.  El momento de la fuerza F vale M = F • d

donde M es momento o torque 

F = fuerza aplicada 

d = distancia al eje de giro 

El torque se expresa en unidades de fuerza-distancia, se mide comúnmente en Newton metro (Nm). 

Si en la figura de la izquierda la fuerza F vale 15 N y la distancia d  mide 8 m, el momento de la fuerza vale: 

M = F  •  d = 15 N  •  8 m = 120 Nm 

La distancia  d  recibe el nombre de “brazo de la fuerza”. 

Una aplicación práctica del momento de una fuerza es la llave mecánica (ya sea inglesa o francesa) que se utiliza para apretar tuercas y elementos similares. Cuanto más largo sea el mango (brazo) de la llave, más fácil es apretar o aflojar las tuercas.  

Con este ejemplo vemos que el torque y la fuerza están unidos directamente.

  

Para apretar una tuerca se requiere cierta cantidad de torque sin importar el punto en el cual se ejerce la fuerza. Si aplicamos la fuerza con un radio pequeño, se necesita más fuerza para ejercer el torque. Si el radio es grande, entonces se requiere menos fuerza para ejercer la misma cantidad de torque.